Fisikawan sama-sama bingung dan penasaran dengan teori Bohr. Mereka mempertanyakan mengapa energi elektron hidrogen terkuantisasi. Atau, mengutarakan pertanyaan dengan cara yang lebih konkret, Mengapa elektron dalam atom Bohr dibatasi untuk mengorbit inti pada jarak tertentu? Selama satu dekade, tidak seorang pun, termasuk Bohr sendiri, yang memiliki penjelasan logis. Pada tahun 1924 Louis de Broglie memberikan solusi untuk teka-teki ini. De Broglie beralasan bahwa jika gelombang cahaya dapat berperilaku seperti aliran partikel (foton), maka mungkin partikel seperti elektron dapat memiliki sifat gelombang. Menurut de Broglie, sebuah elektron yang terikat pada inti berperilaku seperti gelombang yang berdiri. Gelombang berdiri dapat dihasilkan dengan memetik, misalnya, senar gitar (Gambar 7.12). Gelombang digambarkan sebagai berdiri, atau diam, karena mereka tidak berjalan sepanjang tali. Beberapa titik pada string, yang disebut node, tidak bergerak sama sekali; yaitu, amplitudo gelombang pada titik-titik ini adalah nol. Ada simpul di setiap ujungnya, dan mungkin ada simpul di antara kedua ujungnya. Semakin besar frekuensi getaran, semakin pendek panjang gelombang "gelombang berdiri" dan semakin besar jumlah node. Seperti yang ditunjukkan Gambar 7.12, hanya ada panjang gelombang tertentu dalam gerakan yang diizinkan dari string.
Gambar 7.12 Gelombang berdiri dihasilkan dengan memetik senar gitar. Setiap titik mewakili sebuah simpul. Panjang string (𝝀) harus sama dengan bilangan bulat total satu setengah panjang gelombang (𝝀/2).
De Broglie berpendapat bahwa jika sebuah elektron berperilaku seperti gelombang yang berdiri dalam atom hidrogen, panjang gelombang harus sesuai dengan keliling orbit dengan tepat (Gambar 7.13). Kalau tidak, sebagian gelombang akan membatalkan sendiri pada setiap orbit berurutan. Akhirnya amplitudo gelombang akan dikurangi menjadi nol, dan gelombang tidak akan ada.
Gambar 7.13 (a) Lingkar orbit sama dengan jumlah panjang gelombang yang tidak terpisahkan. Ini adalah orbit yang diizinkan. (b) Lingkar orbit tidak sama dengan jumlah panjang gelombang integral. Akibatnya, gelombang elektron tidak menutup dengan sendirinya. Ini adalah orbit yang tidak diizinkan.
Hubungan antara keliling orbit yang diizinkan (2𝝅r) dan panjang gelombang (𝝀) elektron diberikan oleh
2𝝅r = n𝝀 (7.7)
di mana r adalah jari-jari orbit, 𝝀 adalah panjang gelombang dari gelombang elektron, dan n = 1, 2, 3,. . . . Karena n adalah bilangan bulat, maka r dapat memiliki hanya nilai-nilai tertentu karena n meningkat dari 1 menjadi 2 menjadi 3 dan seterusnya. Dan karena energi elektron bergantung pada ukuran orbit (atau nilai r), nilainya harus dikuantisasi.
Alasan De Broglie mengarah pada kesimpulan bahwa gelombang dapat berperilaku seperti partikel dan partikel dapat menunjukkan sifat mirip gelombang. De Broglie menyimpulkan bahwa partikel dan sifat gelombang terkait dengan ekspresi
di mana 𝝀, m, dan u adalah panjang gelombang yang terkait dengan partikel yang bergerak, massanya, dan kecepatannya, masing-masing. Persamaan (7.8) mengimplikasikan bahwa partikel yang bergerak dapat diperlakukan sebagai gelombang, dan gelombang dapat menunjukkan sifat-sifat partikel. Perhatikan bahwa sisi kiri Persamaan (7.8) melibatkan sifat panjang gelombang seperti panjang gelombang, sedangkan sisi kanan membuat referensi ke massa, sifat seperti partikel yang jelas.
Contoh 7.5 menunjukkan bahwa meskipun persamaan de Broglie dapat diterapkan pada sistem yang beragam, sifat-sifat gelombang menjadi dapat diamati hanya untuk objek submikroskopik.
Contoh 7.5
Hitung panjang gelombang "partikel" dalam dua kasus berikut: (a) Servis tercepat dalam tenis adalah sekitar 150 mil per jam, atau 68 m/s. Hitung panjang gelombang yang terkait dengan bola tenis 6,0 x 10² kg yang bepergian dengan kecepatan ini. (b) Hitung panjang gelombang yang terkait dengan elektron (9,1094 x 10⁻³¹ kg) bergerak pada 68 m/s.
Strategi
Diketahui massa dan kecepatan partikel dalam (a) dan (b) dan diminta untuk menghitung panjang gelombang sehingga kita membutuhkan Persamaan (7.8). Perhatikan bahwa karena satuan konstanta Planck adalah J.s, m dan u harus masing-masing dalam kg dan m/s (1J = 1 kgm²/s²).
Penyelesaian
(a) Menggunakan Persamaan (7,8) kami menulis
Catatan:
Ini adalah panjang gelombang yang sangat kecil mengingat ukuran atom itu sendiri berada di pangkat 1 x 10⁻¹⁰ m. Karena alasan ini, sifat gelombang bola tenis tidak dapat dideteksi oleh perangkat pengukur yang ada.
(b) Dalam hal ini,
Catatan:
Panjang gelombang ini (1,1 x 10⁻⁵ m atau 1,1 x 10⁴ nm) berada di wilayah inframerah. Perhitungan ini menunjukkan bahwa hanya elektron (dan partikel submikroskopik lainnya) yang memiliki panjang gelombang yang dapat diukur.
Latihan
Hitung panjang gelombang (dalam nanometer) dari atom H (massa = 1,674 x 10⁻²⁷ kg) bergerak pada 7,00 x 10² cm/s.
Tak lama setelah de Broglie memperkenalkan persamaannya, Clinton Davisson dan Lester Germer di Amerika Serikat dan G. P. Thomson di Inggris menunjukkan bahwa elektron memang memiliki sifat mirip gelombang. Dengan mengarahkan seberkas elektron melalui selembar kertas emas tipis, Thomson memperoleh satu set cincin konsentris pada layar, mirip dengan pola yang diamati ketika sinar X (yang merupakan gelombang) digunakan. Gambar 7.14 menunjukkan pola aluminium.
Gambar 7.14 (a) pola difraksi sinar-X dari aluminium foil. (b) Difraksi elektron aluminium foil. Kesamaan kedua pola ini menunjukkan bahwa elektron dapat berperilaku seperti sinar X dan menampilkan sifat gelombang.
Ulasan Konsep
Kuantitas manakah dalam Persamaan (7.8) yang bertanggung jawab atas fakta bahwa objek makroskopik tidak menunjukkan sifat gelombang yang dapat diamati?




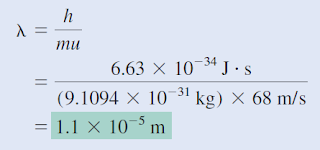













No comments:
Post a Comment
Note: Only a member of this blog may post a comment.